Cooperation is everywhere

From the simplest living things to fundamental mathematical descriptions

In the earliest history of life-as-we-know-it on earth, chemicals floated in a primordial soup. These chemicals interacted with each other in as-yet incompletely understood ways, slowly building in complexity, and eventually building life. The process of building up greater complexity involved chemicals interacting, or working together. Obviously, not all interaction is cooperation, but interaction is fundamental to everything necessary for life, at every scale. Clearly, the first question to ask about cooperation is, what is it? That is, when is an interaction cooperation, and what does that mean?

The dictionary definition is “to work or act together toward a common end or purpose” - but this makes lots of assumptions about why and how cooperation occurs. And in this chapter, we’ll try to discover what exactly qualifies as cooperation. To get there, it will be useful to talk about a little bit of math, then move to biology and evolution, and then towards the end, finally look at human cooperation, and set the stage for a lot of what I want to talk about later.

We can start by looking at cooperation as math. This may seem like an odd starting point, but mathematicians build models of reality, abstracted from the actual thing. If we understand how cooperation works this way, we can see how it applies everywhere. For arithmetic, things are abstracted into units that can be counted, multiplied, and divided. It doesn’t matter which things are being abstracted - if we get the ideas right, we can count mice or men the same way, and correspondingly, see that cooperation for mice and men is the same. This has a certain beauty to it--if you count things correctly, you'll always get the same answer. And you’re pretty unlikely to disagree with someone else about arithmetic, once you both know the rules. 

In the real world, though, not everything works as simply as naive mathematical formulas lead us to expect. Adding one carrot and another will get you two carrots, but adding one puddle of water and another puddle of water gets you a larger puddle - and “adding” one rabbit to another rabbit sometimes gets you many more than two rabbits. So we need to be careful, and start with simple cases, then make sure we don’t misapply the rules or run into exceptions.

Games are simple and concrete ways that people interact in well-defined ways, and once someone thinks about it, it’s fairly easy to turn many games into mathematics. That’s why “game theory” is what mathematicians call the abstractions they use to understand interaction. Like arithmetic, which starts with simple rules, the mathematical theory of cooperation starts with simple games. 

Simple games are easy to describe - at least one player gets at least a single decision, and after the decisions are made, someone wins, or gets some number of points. In more complex scenarios, such as if the players take turns repeatedly, or the allowed moves depend on what the other player has done, or there are random factors, strategy can become very complex, but the mathematical description of the game is still straightforward.

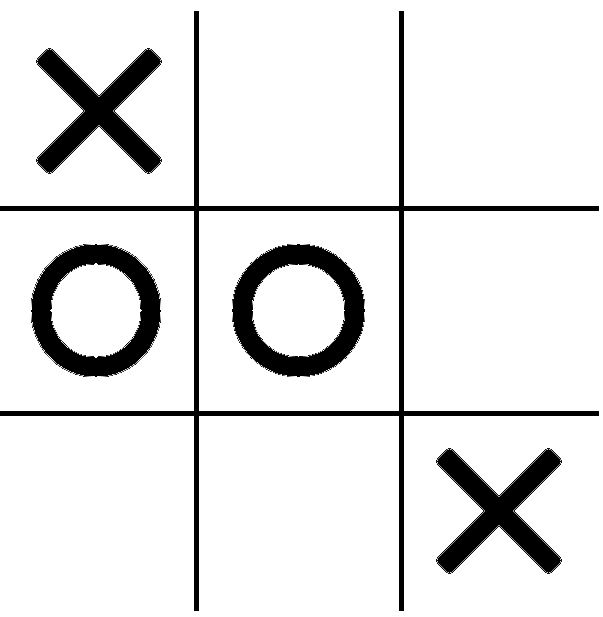
Game theory doesn’t just describe games, though - it can tell us which strategies are best, or whether one of the players can guarantee a win. A game of tic-tac-toe is two players alternating turns, ending when either one player gets three in a row and wins, or the board is full, and no-one wins. Once the game is formalized, it is possible to prove that some moves will allow a player to force a win, or a draw, and others don’t. 

Faced with the above board, if player X plays next, they can choose to go in the center right square and block O. If X goes anywhere else, O can take the spot and win. But if X plays well, this game leads to a tie - O will next need to go in the top right corner to block X from winning, then X must go in the bottom left to stop player O from doing the same, and so on.

But games can be more involved, and strategies rapidly get more complex as games get longer, larger, involve more players, and have more complex rules. Despite complexity, the basic idea is that players each choose what to do to try to win. And one obvious question that game theory tries to answer is how the players can do best, and depending on the game, the answer to which strategy is best can be anywhere from simple, in the tic-tac-toe game above, to impossibly complex, to situations which are dependent on the other player’s willingness to cooperate.

We’ll get back to these questions when we start talking about strategy and cooperation, but one of the simplest types of game is called cooperation games. We’ll start off with a simple case, and say that each player has a choice, and they are better off agreeing. For example, a person wants to go to the theater and watch a movie with friends. As long as they can agree on which movie to watch, they win. (If they are really good at cooperating, they can even split the popcorn!) On the other hand, if Bob wants to watch the latest Marvel movie and John wants to see a romantic comedy, then a failure to cooperate means they end up staying home.

But game theory isn’t usually popcorn and movies. Probably the most famous application of game theory was about the most serious problems humankind has ever faced. During the cold war, the proliferation of nuclear weapons meant that the United States and its allies, and the USSR and its allies, had nuclear weapons pointed at one another. Each side worried that the other might want to start a war, if they thought they could win.

In game theoretic terms, the “solution” was mutually-assured destruction, or MAD - so called in part because the idea was that you’d need to be crazy to start a war once you knew that everyone would lose. As long as everyone knew that each side could retaliate and wipe out the other if attacked, neither side would attack - which meant that you needed to build enough nuclear weapons to win a war in order to keep the peace. But this isn’t usually what we think of as cooperating - even though it probably qualifies as “working or acting towards a common purpose”.

In fact, mutually assured destruction leaves everyone worse off than they started. And to return to our popcorn and movies, we can look back to 1983. The movie “War Games” came out that year, and the plot centers around a computer which is prompted to figure out how to “win” in a nuclear war. (Spoiler alert - if you haven’t seen the movie yet, now’s your last chance before I ruin the ending.) 

The climax of the movie occurs as the artificial intelligence which America evidently put in charge of systems that can launch nuclear weapons, concludes that “The only winning move is not to play.” We’ll need to get back to the artificial intelligence part later, but the conclusion of the movie still remains bleak. We have a heartwarming conclusion where a young Matthew Broderick saves the day - but this leaves humanity still poised at the brink of nuclear catastrophe, at the height of the cold war, forced into building nuclear weapons to stave off a nuclear war.

As the movie notes, the winning move in nuclear war is not to have one, but an even better move during escalating nuclear stalemates is not to keep building more and better weapons, but to stop, or even to back down. All of the effort which goes into building larger, faster, or better hidden nuclear weapons just to maintain a stalemate leaves everyone worse off than if we had spent that money on almost anything else. We can maintain the nuclear stalemate with half as many weapons. With that understood, negotiations to decrease the size of nuclear stockpiles have been proposed and attempted for most of a century, with only a little bit of success. It turns out that even in the face of destruction, human cooperation is quite limited.

But not all negative interactions involve mutually assured destruction. In fact, most modern wars are lose-lose situations, where both sides end up poorer and worse off after the war than they were beforehand. And this doesn’t just go for wars in the traditional sense.  As we’ll discuss in other posts, economic warfare, trade wars, and competition for a fixed pool of resources can be similar. In each case, cooperation is possible and conflict is worth avoiding as long as both sides will inevitably lose - but as soon as one side thinks they have a chance to win, or thinks that losing is worthwhile as long as they hurt the other side, we need something more than just game theory to ensure peace. We need cooperation.

So obviously, people can cooperate, or fail to do so - and then either compete to win, or interact negatively, so everyone loses. And as I’ll propose below, this possibility of noncooperation is a critical part of an interaction being cooperation.

But we haven’t yet discussed who is doing the cooperation. If you want to know whether humans can cooperate with computers, or aliens, or even each other, you probably need to know who or what is able to cooperate - or can fail to do so. Some have claimed that war is uniquely human, but if you look at ants, chimpanzees, or lions, it’s not true. And that makes sense, since the game theory logic applies everywhere. Others want to say that only humans can truly cooperate - but that’s false as well. Clearly, at least some animals cooperate - and as I’ll talk about soon, arguably, even the simplest living things do something a lot like cooperating.